| |
Student: Garrick Ing, M.Eng Student
Supervisor: Prof. Mark Coates
Abstract: Click here
Background:
- The goal of many sensor networks is to detect and track changes (e.g. of an object) in a monitored environment.
- Important to design sequential algorithms that can dynamically fuse the information recorded by the sensors.
- The algorithm should not require excessive exchange of either data or algorithmic information between sensors.
- Goal is to minimize the battery power needed to operate the network and extend the lifetime of the network while maintaining accuracy.
- We present a novel tracking algorithm
- based on the powerful particle filtering framework
- performs the estimation in a distributed fashion to substantially reduce information transfer.
Particle Filter
- We use a sequential Monte Carlo (or particle filtering) method to track the state of the system (the object position).
- These methods maintain a set of "particles", or candidate state descriptions.
- At each time step, the particle filter evaluates how well each particle
(i) conforms to the dynamic model and
(ii) explains the measurement.
- The method eliminates the need for any centralized processing by using nodes in the sensor network to keep track of the state of the system.
Sensor Network Architecture
- The architecture is composed of clusters of nodes.
- Each cluster consists of a class A node (the cluster head) and several class B sensor nodes.
- Class A nodes: computationally powerful nodes which have more energy resources and controls class B nodes.
- Class B nodes: responsible for sensing the monitored environment and reporting their measurements to their single parent class A node.
- All class A nodes maintain a common particle filter.
- When a class B node makes a measurement, it transmits the data to its parent class A node.
- The class A node uses its particle filter to adaptively quantize the measurement for distribution to the other class A nodes.
- Other class A nodes decode the quantized information using the particle filter.
- All class A nodes use decoded data to propagate the particle filter.
- Results in a 4-5 fold compression in data exchange with minimal reduction in estimation accuracy.
Data-encoding Distributed Estimation
- Simulated an object moving through a sensor field according to specified dynamics (Jump-state Markov system).
- Object turns left, turns right, or goes straight at each time step.
- Sensor field comprises of 16 class A nodes and 128 class B nodes.
- 8 class B sensors measure distance to object (plus distance-dependent noise) at any time instant.
Results
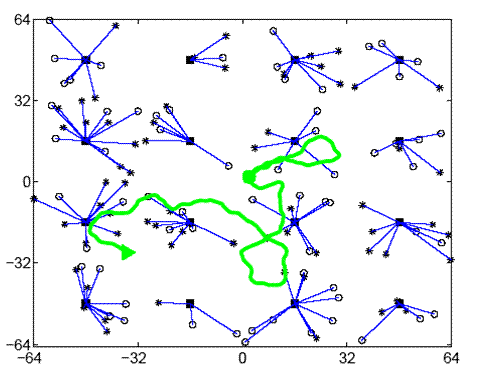
Figure 1: Example of a clustering network. Solid squares indicate class A nodes. Circles and stars are class B distance-measurement nodes. Thin lines represent the class A parent of each class B node. The thick line indicates an example trajectory of the object over 500 times steps, starting at the circle and moving to the triangle.
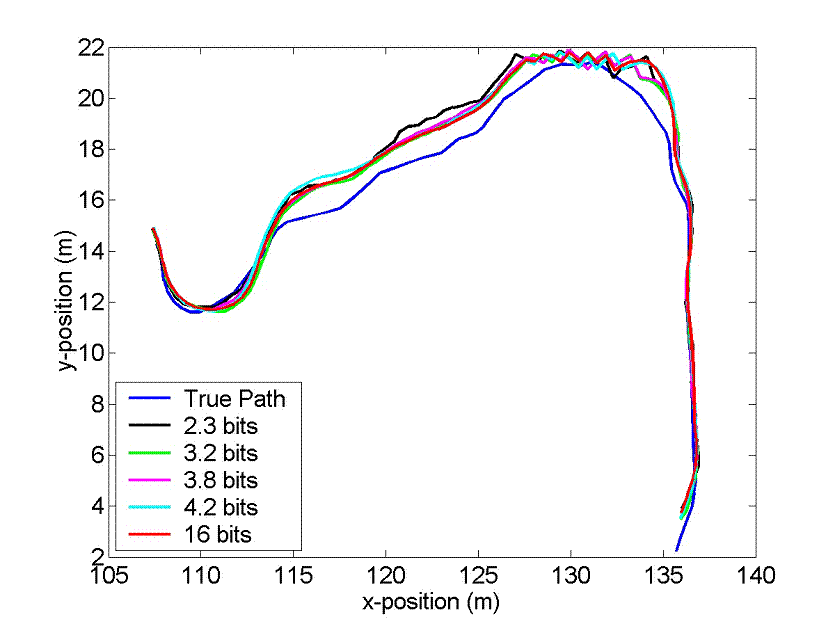
Figure 2: An example of 100 time steps of the true trajectory and the 5 estimates using various number of bits.
Current Investigations
- To minimize the amount of communication needed between the class A nodes. This can be achieved by quantized vectorization of the data such that sensor data will be transmitted to the other nodes periodically.
- To develop a working hardware sensor network model. Initial testing using the Crossbow MICA2 wireless sensor network were not successful because of the hardware limitation. We are currently building our network with newly designed hardly and conducting tests on it. Some undergraduate students are helping out with the model.
|



