COMPUTER NETWORKS RESEARCH LAB

Department of Electrical and Computer Engineering, McGill University

NAVIGATION Home People Photos     RESEARCH Projects Publications     LINKS AAPN MITACS McGill TSP McGill ECE     LOCAL ACCESS Local Info

Project Descriptions Return to Network Monitoring Projects Code Available! Download Optimization and Analysis of Distributed Averaging with Short Node Memory   Researchers: Boris Oreshkin Ph.D. Student, Prof. Mark Coates, Prof. Michael Rabbat 1 Description Distributed averaging describes a class of network algorithms for the decentralized computation of aggregate statistics. Initially, each node has a scalar data value, and the goal is to compute the average of these values at every node (the so-called average consensus problem). To accomplish this task, nodes iteratively exchange information with their neighbors and perform local updates until the value at every node converges to the initial network average. Much previous work has focused on one-step algorithms where each node maintains and updates a single value; every time an update is performed, the previous value is forgotten. Within this framework, convergence to the average consensus is achieved asymptotically. The convergence rate is fundamentally limited by network connectivity, and it can be prohibitively slow on topologies such as grids and random geometric graphs, even if the update rules are optimized. In this paper, we demonstrate, both theoretically and by numerical examples, that adding a local prediction component to the update rule can significantly improve the convergence rate of distributed averaging algorithms. We focus on the case where the local predictor is a linear combination of the node’s two previous values (i.e., two memory taps), and our update rule computes a combination of the predictor and the usual weighted linear combination of values received from neighbouring nodes. We derive the optimal mixing parameter for combining the predictor with the neighbors’ values, and carry out a theoretical analysis of the improvement in convergence rate that can be obtained using this acceleration methodology. For a chain topology on n nodes, this leads to a factor of n improvement over the one-step algorithm, and for a two-dimensional grid, our approach achieves a factor of n1∕2 improvement, in terms of the number of iterations required to reach a prescribed level of accuracy. 2 Problem Formulation We assume that a network of n nodes is given, and that the communication topology is specified in terms of a collection of neighborhoods of each node: 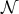i ⊆{1,…,n} is the set of nodes with whom node i communicates directly. For j 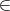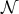i, we will also say that there is an edge between i and j, and assume that connectivity is symmetric. We furthermore assume that the network is connected. Initially, each node i = 1,…,n has a scalar value xi(0) 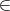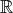, and the goal is to develop a distributed algorithm such that every node computes 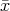= 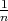∑ i=1nx i(0). Previous studies (see, e.g.,  [Xiao and Boyd, 2004]) have considered linear updates where ∑ jWij = 1, and Wi,j≠0 only if j 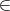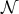i. One network iteration of the algorithm is succinctly expressed as the linear recursion x(t) = Wx(t - 1). Let 1 denote the vector of all ones. For this setup,   [Xiao and Boyd, 2004] have shown that necessary and sufficient conditions on W which ensure convergence to the distributed average consensus (DAC), are where J is the averaging matrix, J = 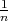11T , and ρ(A) denotes the spectral radius of a matrix A: ρ(A) ≜ max i{|λi| : i = 1, 2,…,n}, where {λi}i=1n denote the eigenvalues of A. Algorithms have been identified for locally generating weight matrices that satisfy the required convergence conditions, e.g., Maximum–degree and Metropolis–Hastings weights (see  [Xiao and Boyd, 2004]). In  [Aysal et al., 2009] , we described a method for accelerating DAC. Its network-wide equations can be expressed in matrix form by defining where I is the identity matrix of the appropriate size and 3 Main Results The following theorem provides a closed form expression for the solution to the problem of mixing parameter optimization. Theorem 1 (Optimal mixing parameter). Suppose θ3 + θ2 + θ1 = 1 and θ3 ≥ 1, θ2 ≥ 0. Suppose further that |λn(W)|≤|λ2(W)|. Then the solution of the optimization problem is given by the following: Below we demonstrate that the rate at which the spectral radius of accelerated operator Φ3[αopt] goes to 1 is significantly slower than that of the non-accelerated one-step operator W. Our main result for the convergence rate of accelerated consensus follows. Theorem 2 (Convergence rate). Suppose the assumptions of Theorem 1 hold. Suppose further that the original matrix W satisfies ρ(W - J) ≤ 1 - Ψ(n) for some function Ψ : ℕ → (0, 1) of the network size n decreasing to 0. Then the operator Φ[αopt] satisfies ρ(Φ[αopt] - J) ≤ 1 -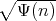. Next, we investigate the gain that can be obtained by using our accelerated algorithm. We adopt the expected gain E{τasym(W)∕τasym(Φ3[αopt])} as a performance metric. The expected gain characterizes the average improvement obtained by running our algorithm over many realizations of the network topology. In this case the spectral gap, Ψ(n), is considered to be a random variable with its value being dependent on the particular realization of the graph. Theorem 3 (Expected gain). Suppose the assumptions of Theorem 1 hold. Suppose further that the original matrix W satisfies E{ρ(W - J)} = 1 - E{Ψ(n)} for some function Ψ : ℕ → (0, 1) of the network size n decreasing to 0. Then we have: The following result is useful for characterizing the improvement in the case of deterministic topologies (grid, chain, etc.). Corollary 1. Suppose that the assumptions of Theorem 3 hold and suppose in addition that ρ(W - J) = 1 - Θ(n-β). Then the improvement in asymptotic convergence rate attained by the accelerated algorithm is polynomial in the size of the network: The following theorem provides the indication of the fact that minimizing the spectral radius is equivalent to minimizing the total averaging time under certain conditions. Theorem 4. Let Φ 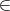n×n be a consensus operator. Suppose that there exists finite T* ℕ such that, for any t ≥ T*, the following holds: Suppose further there exists some 0 < c < 1 such that Then for ε → 0, 4 Numerical Experiments and Discussion Figure 1 compares the MSE curves for the proposed algorithm with the optimal one-step matrix of  [Xiao and Boyd, 2004] and two versions of polynomial filter consensus of  [Kokiopoulou and Frossard, 2009], one using 3 taps and the other using 7 taps. We see that in the RGG scenario (Fig. 1(a)), our algorithm outperforms the optimal one-step matrix and polynomial filter with 3 memory taps and converges at a rate similar to that of the 7-tap version of polynomial filter (The calculation of optimal weights in the polynomial filter framework quickly becomes ill-conditioned with increasing filter length, and we were not able to obtain stable results for more than 7 taps on RGG topologies. Note that in their paper,   [Kokiopoulou and Frossard, 2009] also focuse on filters of length no more than 7.). We conclude that for RGGs, our algorithm has superior properties with respect to polynomial filter since it has better error performance for the same computational complexity, and our approach is suitable for completely distributed implementation. Moving our attention to the chain topology (Fig. 1(b)) only emphasizes these points, as our accelerated algorithm significantly outperforms even the 7-tap polynomial filter. 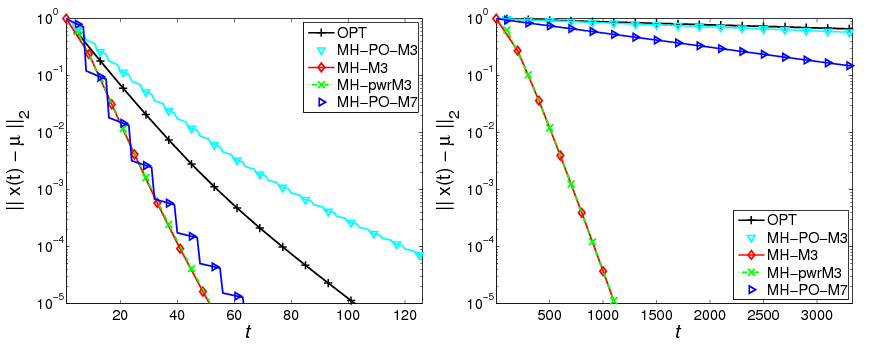Figure 1: MSE versus time step for the consensus algorithms, n = 200. Optimal weight matrix (OPT): +; optimal polynomial filter with 3 taps (MH-PO-M3): ▽, 7 taps (MH-PO-M7): ⊳; proposed accelerated consensus (M = 3 and MH matrix) with known λ2(W) (MH-M3): ◇ and with the online estimation of λ2(W) (MH-pwrM3): ×. (a) Random Geometric Graph (on the left). (b) Chain Graph (on the right) To investigate the robustness and scalability properties of the proposed algorithm, we next examine the processing gain, Tave(WMH)∕Tave(Φ3[α*]), with respect to the MH matrix. We see from Fig. 2(a) that in the RGG setting, the proposed algorithm always outperforms DAC with the optimal weight matrix and polynomial filter with equal number of memory taps, and our approach scales comparably to 7-tap polynomial filter. On the other hand, in the chain graph setting (Fig. 2(b)) the proposed algorithm outperforms all the competing algorithms with the gain (w.r.t. the MH matrix) scaling linearly with n. These results confirm that it is possible to implement the accelerated DAC in a completely distributed fashion and still obtain significant processing gains that scale well with the size of the network and match those theoretically predicted for the optimal (oracle) algorithm. 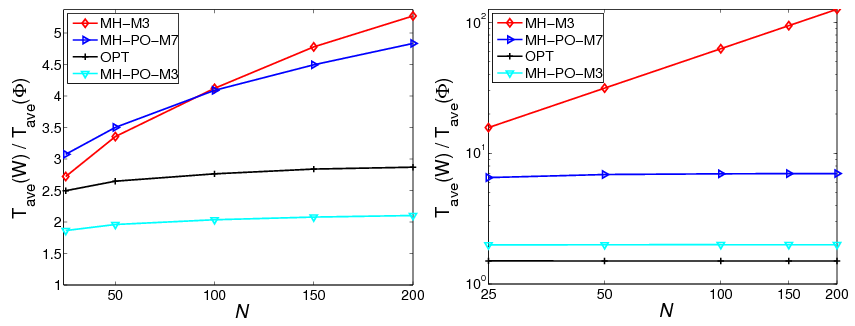Figure 2: Processing gain. Optimal weight matrix (OPT): +; optimal polynomial filter with 3 taps (MH-PO-M3): ▽, 7 taps (MH-PO-M7): ⊳; proposed accelerated consensus, M = 3 with known λ2(W) and MH matrix (MH-M3): ◇. (a) Random Geometric Graph (on the left). (b) Chain Graph (on the right) References [Aysal et al., 2009]   Aysal, T., Oreshkin, B., and Coates, M. (2009). Accelerated distributed average consensus via localized node state prediction. to appear, IEEE Trans. Sig. Process. [Kokiopoulou and Frossard, 2009]   Kokiopoulou, E. and Frossard, P. (2009). Polynomial filtering for fast convergence in distributed consensus. IEEE Trans. Sig. Process., 57(1):342–354. [Tsitsiklis, 1984]   Tsitsiklis, J. (1984). Problems in Decentralized Decision Making and Computation. PhD thesis, Massachusetts Institute of Technology. [Xiao and Boyd, 2004]   Xiao, L. and Boyd, S. (2004). Fast linear iterations for distributed averaging. Systems and Control Letters, 53(1):65–78. Publications: B.N. Oreshkin, M.J. Coates, and M.G. Rabbat, Optimization and analysis of distributed averaging with short node memory. arXiv:0903.3537v1; available at http://arxiv.org/abs/0903.3537v1.