|
Possible Applications:
The algorithm is intended to operate on traffic statistics collected (in
distributed manner) at core nodes of large backbone networks, such as the 11
core routers of the
Abilene network.
At each timestep t, the algorithm requires as inputs a traffic
measurement vector xt and an associated scalar yt.
An example choice for xt is the flow vector (the
number of packets or bytes in each source-destination flow) and for yt
the total number of packets in the network, as recorded during the
measurement interval corresponding to timestep t.
Kernel Recursive Least Squares
The recursive least squares algorithm is a popular method of obtaining
linear predictors of a data sequence. It is suitable for online learning
scenarios as it observes input samples sequentially and has modest storage
and computational requirements. It does not need to store historical data
and its computational cost per timestep is independent of time.
Kernel machines use a kernel mapping function to produce non-linear and
non-parametric learning algorithms
[4]. The idea behind kernel machines is that a suitable kernel
function, when applied to a pair of input data vectors, may be interpreted
as an inner product in a high dimensional Hilbert space known as the feature
space
[3]. This allows inner products in the feature space (inner products of
the feature vectors) to be computed without explicit knowledge of the
feature vectors themselves, by simply evaluating the kernel function:
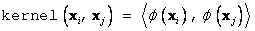
where xi , xj denote
input vectors and j represents the
mapping onto the feature space.
Popular kernel functions include the Gaussian kernel with variance
s2:
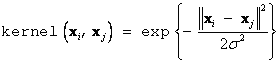
and the polynomial kernel of degree d:
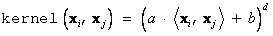
A special case of the polynomial kernel is the linear kernel:
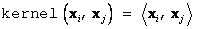
Note that the linear kernel is simply the inner product (dot product) of
its arguments.
The Kernel Recursive Least Squares (KRLS) algorithm combines the
principles of recursive least squares and kernel machines, providing an
efficient and non-parametric approach for performing online data mining and
anomaly diagnosis.
The Key Idea:
The objective of the Kernel-based Online Anomaly Detection (KOAD)
algorithm is to build a dictionary
of input vectors, such that the mapping of the input vectors onto the
feature space forms an approximately linearly independent basis in
the feature space
[3].
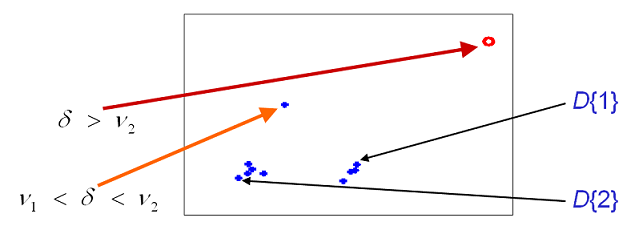
Fig.1: Simplified depiction of
space spanned by 2 sample dictionary
elements, D{1} and
D{2}.
d is a distance metric, and
n1,
n2 are thresholds where
n1 <
n2. When d >
n2, we infer that the
current observation is too far away from the space of normality as defined
by the dictionary, and instantly declare a red
alarm; when n1
< d <
n2, we raise an
orange alarm, keep track of the
usefulness of the arriving xt for a short interim
period, and then take a firm decision on it.
Outline of KRLS Anomaly Detection Algorithm:
The algorithm proceeds by evaluating the degree of linearly
dependence of the feature vector at each timestep t,
j(x(t)), on the
current dictionary. The algorithm evaluates
dt, the error in projecting the current feature vector
onto the dictionary, according to:
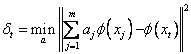
where x1...xm represent
members of the dictionary at timestep t. The value of
dt is then
compared with the thresholds n1
and n2 to initiate the
immediate relevant response, as shown in Fig.2. A complete description of
the algorithm is provided in the associated technical report
[6].
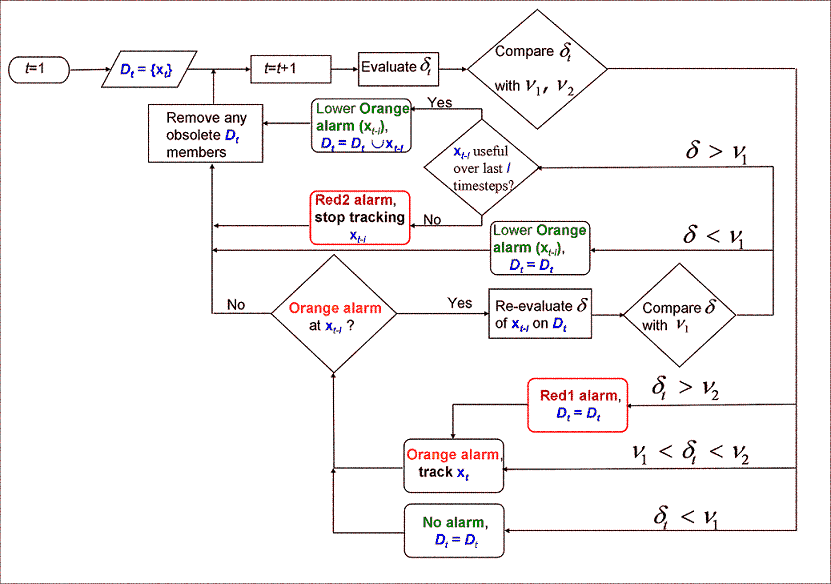 Fig.2: Overview
of KRLS online anomaly detection algorithm. Detailed description is provided
in
[6].
|
Return to Network Monitoring Projects